Find the Principal Stresses and the Orientation of the Axes

By Jo_Lauryn863 24 Apr, 2022 Post a Comment

Since the stress tensor is a. Draw a set of coordinate axes with σ x1 as abscissa positive to the right and τ x1y1 as ordinate positive downward.

Mechanics Of Materials Lecture 19 Principal Stresses And Maximum In Plane Shear Stress Youtube

It also draws an approximate Mohrs cirlce for the given stress state.

. The largest value of of sigma is the first principal stress and the smallest. For anisotropic materials this is not the case in general. Find the principal stresses and the orientation of the principal axes of stress for the following cases of plane stress.

Therefore one of the principal stress axes must be vertical and increase with depth as the rock overburden lithostatic pressure increases. Oye 20000 psi 9 25000 ps 5x 15000 psi c. Segment 1 of lecture 2.

Given the stress components s x s y and t xy this calculator computes the principal stresses s 1 s 2 the principal angle q p the maximum shear stress t max and its angle q s. Into the equation for shear stress. The state of plane stress at a point on a body is represented on the element shown in the Figure.

The maximum shear stress isτ max σ c σ a2. Principal stresses are maximum and minimum value of normal stresses on a plane when rotated through an angle on which there is no shear stress. Principal Plane It is that plane on which the principal stresses act and shear stress is zero.

Thus the vertical and horizontal relative stress magnitudes and the horizontal stress orientations can be derived from the principal strain orientations and magnitudes. Hide Text 32 An alternative method for determining principal stresses the maximum shear stress and the principal directions is to construct a. Hide Text 31 Voilá.

0 σyy σxxsinθP cosθP τ xycos2θP sin2θP 0 σ y y σ x x sin. To find the maximum shear stress and the particular plane you are helped by the following theorem. The principal stresses are the characteristic values or eigenvalues of the stress tensor t ij.

Find the principal stresses and the orientation of the principal axes for the following cases of plane stress. The normal and shear stress acting on the right face of the plane make up one point and the normal and shear stress on the top face of the plane make up the second point. In 2-D the principal stress orientation θP θ P can be computed by setting τ xy 0 τ x y 0 in the above shear equation and solving for θ θ to get θP θ P the principal stress angle.

σ- 50000 psi b. Mechanical Engineering questions and answers. No shear stress acts on this element.

The other two stress axes are horizontal. 2 𝑖 2𝜃𝜏 𝑐 2𝜃 𝜏 2090 2 𝑖 4749𝜏 𝑐 4749 xy. Locate point A representing the stress conditions on the x face of the element by plotting its coordinates σ x1 σ x and τ x1y1 τ.

0 σyy σxxsinθP cosθP τ xycos2θP sin2θP 0 σ y y σ x x sin. Locate the centre of the circle c at the point having coordinates σ x1 σ avg and τ x1y1 0. τ max acts on a plane with the normal vector 45 from the principal directions n a and n c.

This can be done by means of our earlier relation between the principal stresses and σ x σ y and τ xy. In 2-D the principal stress orientation θP θ P can be computed by setting τ xy 0 τ x y 0 in the above shear equation and solving for θ θ to get θP θ P the principal stress angle. Include the Mohrs circle to your answer a ox 40MPa 0 0 Txy 80MPa b ox 140MPa Oy20MPa Txy- 60MPa C 0 -120MPa 50MPa Txy 100MPa d 0x 10MPa 0 - 4MPa Txy 8MPa e Ox -10MPa Oy 20MPa Txy -6MPa.

9 65000 psi gu 10000 psi 7500 psi b. Find the principal stresses and the orientation of the axes of principal stress with the x y axes for the following situations. Differentiate the Eqn2 Eqn3 with respect to θ and equate it to zero.

Include the Mohrs circle to your answer a 0x 40MPa 0 0 Txy 80MPa b 0x 140MPa Oy20MPa Txy - 60MPa c 0x-120MPa y 50MPa Txy 100MPa d 0x 10MPa 0 - 4MPa Txy 8MPa e Ox -10MPa y 20MPa Txy -6MPa. We can eliminate theta by squaring both sides and adding them I have taken the liberty to transpose the first term on. Txy 100 MNm2 Write a simple computer code.

σ- 5000 psi С. Substituting this into the maximum shear equation above gives the desired result. You will get the equations for maximum and minimum values.

The equations describing stress transformation are the parametric equations of a circle. There are two values of lying between and which satisfy the above equationThese specify the angles that the two mutually orthogonal principal axes lying in the -plane make with the -axisHence we have now determined the directions of all three principal axes. Find the principal stresses and the orientation of the principal axes for the following cases of plane stress.

Still it is possible at least in principle to determine a failure surface in the stress space by performing experiments along different stress paths. 0 Txy c 0x a Ox 40 MNm² Oy 80 MNm2 b ox 70 MNm² oy 30 MNm² Txy 60 MNm2 --120 MNm² Oy 50 MNm. The principal strain axes are assumed to define the principal in-situ stress axes and the relative strain magnitudes are assumed to correspond to the relative stress magnitudes.

State it is known empirically that yielding first occurs on a plane with maximum shear stress. Incidentally once we have determined the orientation angle of a principal axis we can then substitute back into. Principal Stresses and Principal AxesCourse webpage with notes.

Principal Angle The orientation of the principal plane with respect to the original axis is the principal angle. For isotropic materials the principal axes of strain and the principal axes of stress coincide. Construct a Mohrs circle of stress for each of the plane-stress condition given above and explained the benefit in metal working.

Our goal for finding the principal stresses on an element is to eliminate the dependence of the stress transformation equations on theta. 𝜏 𝜎 𝜎. The maximum and minimum normal stress principal stress will be.

However such a failure surface will depend on the orientation of the anisotropic. ơ- 5000 psi С. The three roots of the stress cubic equation 133 are the principal stresses corresponding to which are three sets of direction cosines which establish the relationship of the principal planes to the origin of the nonprincipal axes.

σ max σ x σ y 2 σ x σ y 22 Txy2Eqn4. The direction of fault movement is such that fracture opens along the minimum stress axis and the slip occurs as the rock wedge containing the maximum stress axis moves inward. Find the Principal stresses and the orientation of the axes of principal stress with the x y axes for the following situation.

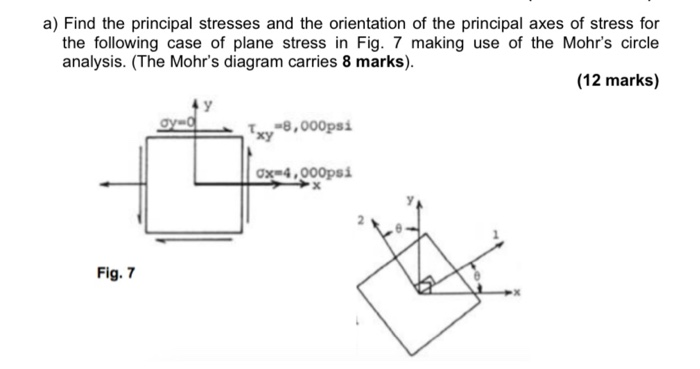
Solved A Find The Principal Stresses And The Orientation Of Chegg Com